题目

给定一个非负整数 n ，请计算 0 到 n 之间的每个数字的二进制表示中 1 的个数，并输出一个数组。

示例 1：

• 输入：n = 2
• 输出：[0,1,1] 解释：
  • 0 --> 0
  • 1 --> 1
  • 2 --> 10

示例 2：

• 输入：n = 5
• 输出：[0,1,1,2,1,2] 解释：
  • 0 --> 0
  • 1 --> 1
  • 2 --> 10
  • 3 --> 11
  • 4 --> 100
  • 5 --> 101

解题思路

针对这个题目，我们有两种方法可以解决，可以使用 奇偶数的二进制特性 或者通过 x = x & (x-1) 来消 去最小位的 1 去求解。

奇偶数的二进制特性

对于偶数： 1的个数等于减半的数的1的个数。

对于奇数： 就是减一的那个偶数的1的个数再加上1。

所以我们可以从 1 开始到 n 进行遍历，将结果存储在 result 变量中，如果 i 为偶数，则直接使用减半的数的 1 的个数即可，如果为奇数，则使用减一的那个偶数的1的个数再加上1。

class Solution {
    public int[] countBits(int n) {
        int[] result = new int[n+1];
        result[0] = 0;
        for(int i = 1; i<=n; ++i){
            result[i] = (i&1) == 1 ? result[i-1]+1 : result[i >> 1];
        }
        return result;
    }
}

消 1 法

通过 x = x & (x-1) 消去最小位的1, 例如：

1. 21的二进制为 0001 0101 ，20的二进制为 0001 0100 & 运算之后为20
2. 再将结果 20 与 19 进行 & 运算，即 0001 0100 & 0001 0011 结果为 16
3. 16 与 15 进行 & 运算，0001 0000 & 0000 1111 结果为0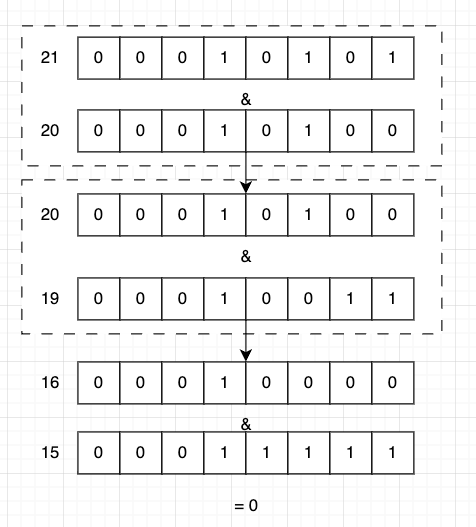

public int[] countBits(int n) {
    int[] result = new int[n+1];
    int temp = 0;
    int x = 0;
    for(int i = 0; i<=n; ++i){
        temp = 0;
        x = i;
        while(x>0){
            ++temp;
            x = x & (x-1);
        }
        result[i] = temp;
    }
    return result;
}